ITパスポート試験のテクノロジ系「基礎理論」では、コンピュータサイエンスの土台となる「集合」や「論理」の知識が問われます。
これらの概念は、一見すると数学のように見えますが、実はデータ管理やプログラミングの条件分岐など、ITのあらゆる分野で活用されています。
この記事では、集合の基本的な考え方や、ベン図を使った集合の操作、そして論理演算の土台となる「命題」について解説します。この知識は、問題解決のための論理的思考力を養う上でも不可欠です。
1. 集合とは?要素の集まりを理解する
集合とは、特定の条件を満たす「要素」の集まりを、明確に区別してひとまとまりにしたものです。
- 要素(Element): 集合を構成する一つ一つのモノや数。
- 例: 「日本の47都道府県」という集合の要素は、東京、大阪、北海道などです。
ベン図を使った集合の可視化
集合の関係を図で表したものを「ベン図」といいます。ベン図を使うと、複数の集合がどのように関わり合っているかを視覚的に理解できるため、ITパスポートの問題を解く上で非常に有効です。
ベン図を用いて、集合の基本的な操作を覚えましょう。
2. 集合の基本操作:和集合と積集合
ITパスポート試験で問われる主な集合の操作は、「和集合」と「積集合」です。
1. 和集合(AまたはB)
和集合とは、集合Aと集合Bのどちらか一方、または両方に含まれる要素の集まりです。
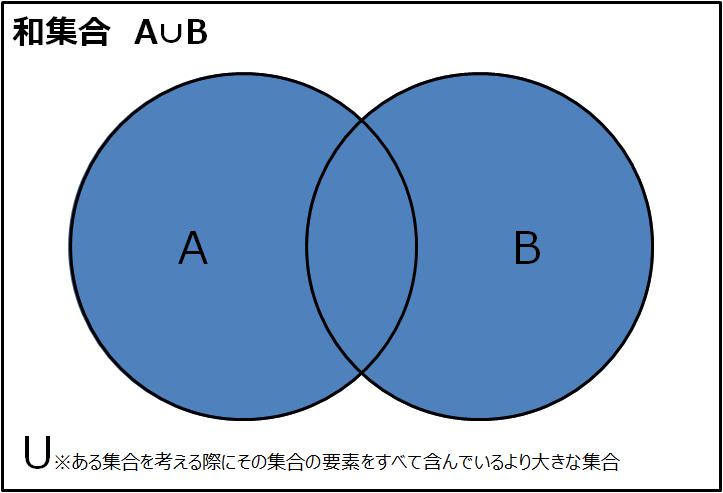
- 記号: A∪B(”A union B” または “AカップB”)
- ベン図: AとBの領域をすべて合わせた部分。
- 論理演算との関係: OR演算(論理和)に対応します。
2. 積集合(AかつB)
積集合とは、集合Aと集合Bの両方に共通して含まれる要素の集まりです。
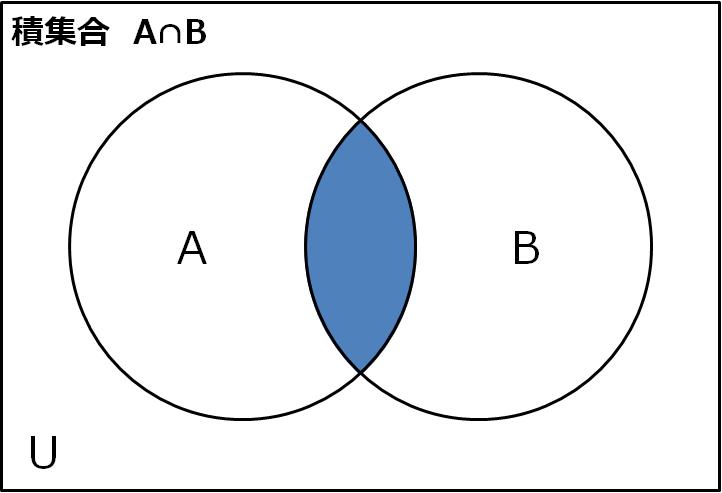
- 記号: A∩B(”A intersect B” または “AキャップB”)
- ベン図: AとBが重なり合っている部分。
- 論理演算との関係: AND演算(論理積)に対応します。
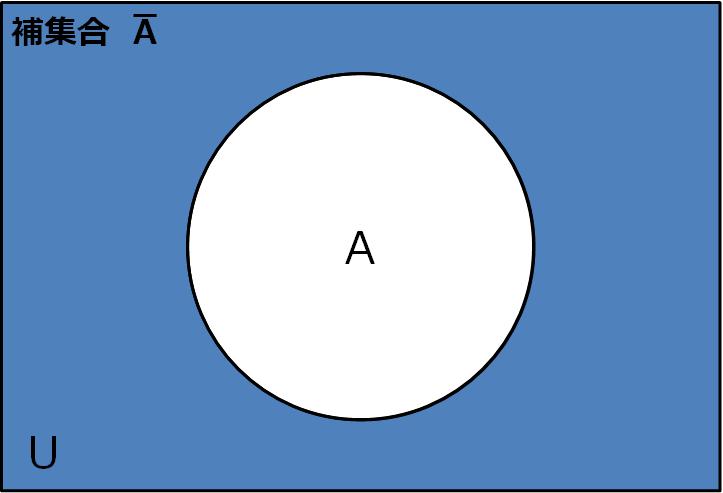
3. 補集合(Aではない)
補集合とは、ある集合Aの要素を含まない、全体の集合(全体集合 U)の中の要素の集まりです。

3. 命題と論理:真偽の判断
命題とは、「真(True)か偽(False)かが明確に判断できる文章や式」のことです。
- 例(命題): 「2 + 3 = 5 である」(真)、「東京タワーの高さは100mである」(偽)
- 例(命題ではない): 「あの花は美しい」(美しさの基準が曖昧)
ITパスポートの論理演算の問題は、この命題の真偽を判断する能力に基づいています。
論理演算の役割
論理演算は、命題の真偽(1または0)を組み合わせた結果を判断するために使われます。
| 演算 | 命題の条件 | 真になる条件 |
| AND | P かつ Q | PもQも真のとき |
| OR | P または Q | PかQのどちらかが真のとき |
| NOT | P ではない | Pが偽のとき |
論理演算について詳しく学ぶには、このシリーズの最重要記事「【最重要】論理演算の基本」に進んでください。集合で使ったベン図が、論理演算でも非常に役立ちます。
4. 集合と論理の関係性(ド・モルガンの法則)
集合と論理演算は、非常に密接に関係しています。その関係性を最も分かりやすく示すのが「ド・モルガンの法則」です。
ド・モルガンの法則は、補集合(NOT)を使った集合の積集合や和集合の関係を、別の形で表すことができる法則です。
ド・モルガンの法則(試験対策)
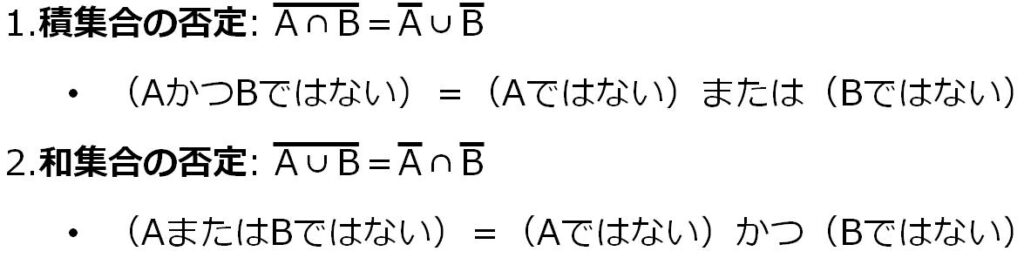
この法則は、「否定(バー)」を分配すると、記号( ∩ や ∪ )が反転すると覚えると、問題に正答しやすくなります。この知識は、論理演算の複雑な問題を解く際の重要なテクニックとなります。
まとめ:集合と論理はITの「土台」
集合と命題の知識は、ITパスポートの出題範囲の中でも、特に計算や論理的思考の基礎となる分野です。
- 集合: データの集まりや、システムの範囲を視覚化(ベン図)して理解する。
- 論理: 命題の真偽(1/0)に基づき、複雑な条件を正確に判断する。
これらの知識は、後のアルゴリズムやデータベースの学習、さらには実務での条件分岐やデータ分析にも役立つ、ITの最も重要な土台です。
このブログの教科書コンテンツで、ITパスポート合格に向けた基礎を徹底的に固めていきましょう。
